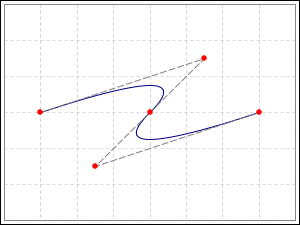
Here's an example that uses quadratic interpolation.
Code: Select all
points = (
((100, 300),),
((400, 300), (550, 450)),
((700, 300), (250, 150))
)
show box at PathMotion(points, 1.0)
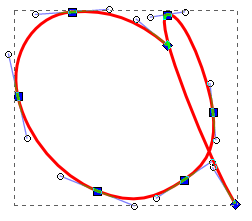
Code: Select all
a_points = (
((485, 238),),
((390, 205), (454, 212), (426, 202)),
((336, 289), (353, 207), (326, 247)),
((415, 384), (345, 331), (378, 369)),
((502, 373), (452, 399), (474, 391)),
((531, 305), (530, 355), (534, 333)),
((485, 208), (528, 276), (503, 205)),
((553, 397), (468, 210), (531, 360))
)
show box at PathMotion(a_points, 5.0)
path ::= (
segment,
{segment,}
segment
)
segment ::= linear-segment | quadratic-bezier-segment | cubic-bezier-segment
# Moves to point in a straight line
linear-segment ::= ( point, [time] )
# Moves to the first point along a quadratic curve, using the second point as the control point
quadratic-bezier-segment ::= ( point, point, [time] )
# Moves to the first point along a cubic curve, using the second and third points as the first and second control points
cubic-bezier-segment ::= ( point, point, point, [time] )
point ::= any form of coordinate that Position can take (a tuple or list of 2 or 4 members)
time ::= float (ideally between 0.0 and 1.0, but not necessarily)
Any time you don't manually specify is linearly interpolated between the previous and following times that are specified. This allows you to specify that at a specific time, the motion will be at a specific point. By default, the start time is 0.0 and the end time is 1.0, unless you specify something different.
To make paths, the easiest thing to do is to use a vector image application (i used Inkscape). This function supports all the same motion types as SVG paths except arcs (a/A). (You may have to manually specify the points that are automatically generated by t/T or s/S.) In time, i might even get around to making a helper script to convert SVG path code to path objects PathMotion can use. For now, you'll have to do it manually.
(If you're using Inkscape, it's easy because Inkscape converts all straight line types (l/L, v/V and h/H) to absolute, arbitrary lines (L), and all curve types (a/A, q/Q, t/T, s/S) to absolute, cubic Bézier lines (C). Of course, this assumes you have a single line path, which you obviously should. All you have to do is copy the "d" code, break it up by segments - easy to do because each segment starts with L or C - then delete the letters, turn all the floating point numbers to ints, and rearrange the coordinates in C lines from [a b c] to .)
Here's how to use it. Make a new renpy (.rpy) file in your game directory, and copy this into it.
[code]
init python:
class PathInterpolator(object):
anchors = {
'top' : 0.0,
'center' : 0.5,
'bottom' : 1.0,
'left' : 0.0,
'right' : 1.0,
}
# Default anchors (from Position)
default_anchors = (0.5, 1.0)
def __init__(self, points):
assert len(points) >= 2, "Need at least a start and end point."
def setup_coordinate_(c):
if len(c) == 2:
c += self.default_anchors
return [ self.anchors.get(i, i) for i in c ]
self.points = []
for p in points:
length = len(p)
if isinstance(p[-1], float):
length = len(p) - 1
point = [ p[-1] ]
else:
length = len(p)
point = [ -1 ]
self.points.append(point + [ setup_coordinate_(p) for i in range(length) ])
# Make sure start and end times are set, if not already set
if self.points[0][0] == -1:
self.points[0][0] = 0.0
if self.points[-1][0] == -1:
self.points[-1][0] = 1.0
# Now we gotta calculate the step times that need calculating
for start in range(1, len(self.points) - 1):
if self.points[start][0] != -1:
continue
end = start + 1
while end < (len(self.points) - 1) and self.points[end][0] == -1:
end += 1
step = (self.points[end][0] - self.points[start - 1][0]) / float(end - start + 1)
for i in range(start, end):
self.points[0] = self.points[0] + step
# And finally, sort the list of points by increasing time
self.points.sort(lambda a, b: cmp(a[0], b[0]))
self.initialized = False
def init_values_(self, sizes):
def to_abs_(value, size):
if isinstance(value, float):
return value * size
else:
return value
def coord_(c):
return [ to_abs_(c[0], sizes[0]) - to_abs_(c[2], sizes[2]),
to_abs_(c[1], sizes[1]) - to_abs_(c[3], sizes[3]) ]
for p in self.points:
for i in range(1, len(p)):
p = coord_(p)
self.initialized = True
def __call__(self, t, sizes):
# Initialize if necessary
if not self.initialized:
self.init_values_(sizes)
# Now we must determine which segment we are in
for segment in range(len(self.points)):
if self.points[segment][0] > t:
break
# If this is the zeroth segment, just start at the start point
if segment == 0:
result = self.points[0][1]
# If this is past the last segment, just leave it at the end point
elif segment == len(self.points) - 1 and t > self.points[-1][0]:
result = self.points[-1][1]
else:
# Scale t
t = (t - self.points[segment - 1][0]) / (self.points[segment][0] - self.points[segment - 1][0])
# Get start and end points
start = self.points[segment - 1][1]
end = self.points[segment][1]
# Now what kind of interpolation is it?
if len(self.points[segment]) == 2: # Straight line
t_p = 1.0 - t
result = [ t_p * start + t * end for i in 0,1 ]
elif len(self.points[segment]) == 3: # Quadratic Bézier
t_pp = (1.0 - t)**2
t_p = 2 * t * (1.0 - t)
t2 = t**2
result = [ t_pp * start + t_p * self.points[segment][2] + t2 * end for i in 0,1 ]
elif len(self.points[segment]) == 4: # Cubic Bézier
t_ppp = (1.0 - t)**3
t_pp = 3 * t * (1.0 - t)**2
t_p = 3 * t**2 * (1.0 - t)
t3 = t**3
result = [ t_ppp * start[i] + t_pp * self.points[segment][2][i] + t_p * self.points[segment][3][i] + t3 * end[i] for i in 0,1 ]
return ( int(result[0]), int(result[1]), 0, 0 )
def PathMotion(points, time, child=None, repeat=False, bounce=False, anim_timebase=False, style='default', time_warp=None, **properties):
return Motion(PathInterpolator(points), time, child, repeat=repeat, bounce=bounce, anim_timebase=anim_timebase, style=style, time_warp=time_warp, add_sizes=True, **properties)
[/code]
Then, you can use it in at clauses just like Move and Position:
[code]
show box at PathMotion((((100, 300),), ((400, 300), (250, 450), 0.25), ((700, 300), (550, 150))), 5.0)
[/code]
Of course, it is a little cryptic to specify your path right in there like that, so you can do this, too:
[code]
python hide:
sine_path = (
((100, 300),),
((400, 300), (250, 450), 0.25),
((700, 300), (550, 150))
)
show box at PathMotion(sine_path, 5.0)
[/code]
Tip: ^_^
When you're moving something around, it might be easier if you use the centre of the image as the anchor.
[code]
a_points = (
((485, 238, 0.5, 0.5),),
((390, 205, 0.5, 0.5), (454, 212, 0.5, 0.5), (426, 202, 0.5, 0.5)),
((336, 289, 0.5, 0.5), (353, 207, 0.5, 0.5), (326, 247, 0.5, 0.5)),
((415, 384, 0.5, 0.5), (345, 331, 0.5, 0.5), (378, 369, 0.5, 0.5)),
((502, 373, 0.5, 0.5), (452, 399, 0.5, 0.5), (474, 391, 0.5, 0.5)),
((531, 305, 0.5, 0.5), (530, 355, 0.5, 0.5), (534, 333, 0.5, 0.5)),
((485, 208, 0.5, 0.5), (528, 276, 0.5, 0.5), (503, 205, 0.5, 0.5)),
((553, 397, 0.5, 0.5), (468, 210, 0.5, 0.5), (531, 360, 0.5, 0.5))
)
show box at PathMotion(a_points, 5.0)
[/code]